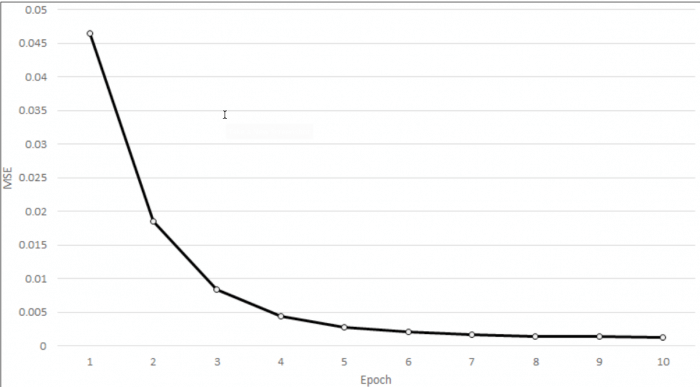
В этой главе мы покажем процесс обучения нейронных сетей, которые выполняются в целях обучения из данных. Мы представляем концепты тренировки, тестировании и валидации и покажем как это реализовать на Java. Мы также покажем несколько методов оценки производительности нейронных сетей в обучении также как и обучение параметров алгоритма. В сумме, в главе мы изучим:
- Процесс обучения
- Алгоритмы обучения
- Типы обучения:
- С учителем
- Без учителя
- Тренировка, тестирование и валидация
- Измерения ошибок
- Обобщение
Способность у обучению нейронных сетей
Что очень замечательно в нейросетях — это их способность к обучению из среды, также как способны одаренные люди. Мы , как люди, обучаемся через наблюдения и повторения, пока некоторые задачи не будут хорошо выполнены. С физиологической точки зрения, процесс обучения в человеческом мозгу — это реконфигурации нейронных соединений между узлами, которые результируются в новую думательную структуру.
Пока соединительная натура нейросетей распространяет процесс обучения по всей структуре, эта особенность делает эту структуру гибкой достаточно, чтобы изучать широкий спектр знаний. В отличие от современных компьютеров, которые могут выполнять только те задачи, на которые они запрограммированы, нейронные системы могут улучшить и выполнять новые действия согласно некоторым удовлетворительным критериям. Другими словами, нейросети не нуждаются в программировании; они обучаются программировать себя.
Как обучение помогает решать проблемы
Принимая во внимание что каждая задача может иметь множество возможных решений, процесс обучения стремится искать оптимальное решение, которое может дать удовлетворительный результат. Использование структур, таких как искуственные нейросети(ANN) поощряется благодаря их способности приобретать знания любых типов, точно принимая входные раздражители, то есть, данные, соответствующие проблеме. Первое, ANN будет производить рандомный результат и ошибку, и основанный на этой ошибке, ANN параметры будут отрегулированы.
Парадигмы обучения
Существуют 2 типа обучения: с учителем и без учителя. Обучение в человеском понимании, например, также работает в этом направлении. Мы можем обучаться из наблюдений без иных паттернов (без учителя), или мы можем иметь учителя, который показывает верный паттерн для слежения(с учителем). Различие между этими парадигмами полагается в основном на актуальности паттерна и меняется от проболемы к проблеме.
Обучение с учителем
Эта категория обучения имеет дело в парах X’; и Y’;, и задача — отобразить их в функции f: X → Y. Здесь Y данная — это учитель, плановые желанные выходы, и X данные — это данные, которые генерируют Y данные. Это аналогично учителю, который обучает всех выполнять определенную задачу, как показано на след. Картинке:
Одна исключительная особенность этой парадигмы обучения — прямая ссылка на ошибку, которая просто сравнивает между плановым и текущим результатом. Параметры сети скармливаются в стоимостную функцию, которая определяет количество несоответсвий между желаемым и текущим выводом.
Обучение с учителем — очень годная для задач, которые заранее предоставляет паттерн, цель достижения. Примеры: классификация картинок, распознавание голоса, функция апроксимации, прогнозирование. Обратите внимание,что нейросеть следует обеспечить предыдущими знаниями парой вводо-независимых значений(X) и выводом классификаци-зависимых значений(Y). Присутсвие зависимых выводом — обязательное условие для обучения с учителем.
Обучения без учителя
В иллюстрированной картинке, в обучении без учителя мы имеем дело только с данными без меток или классификации; вместо этого наша нейронная структура пытается нарисовать логические умозаключения и извлечь знания из этого используя только входные данные X.
Это аналогично самообучению когда кто-то обучает его/ее благодаря его/ее опыту и устанавливая побочные критерии. в обучении без учителя мы не определяем желаемый паттерн для каждого наблюдения но нейронная структура может обучаться без какого-либо учителя.
Здесь, функция стоимости(cost function) играет важную роль. Она сильно воздействует на значения нейрона так же хорошо как и связь между входными значениями.
Примеры задач, где используется обучение без учителя: кластеризация, компрессия данных, статистические модели и языковые модели. Эта обучающая парадигма покрывается глубже в четвертой главе: Самоорганизующиеся карты(Self-Organizing Maps).
Систематическое структурирование — алгоритм обучения
Пока что мы определили процесс обучения и как он выполняется. Однако на практике мы должны углубиться немного глубже в математическую логику, в сам алгоритм обучения. Алгоритм обучения — это процедура, которая управляет процессом обучения нейронных сетей и сильно определена архитектурой нейронной сети. С математической точки зрения, один хочет найти оптимальные веса W, которые могут привести функцию стоимости(cost function) C(X,[Y]) к минимально возможному значению.
В основном этот процесс выполнения представлен в следующей блок-схеме:
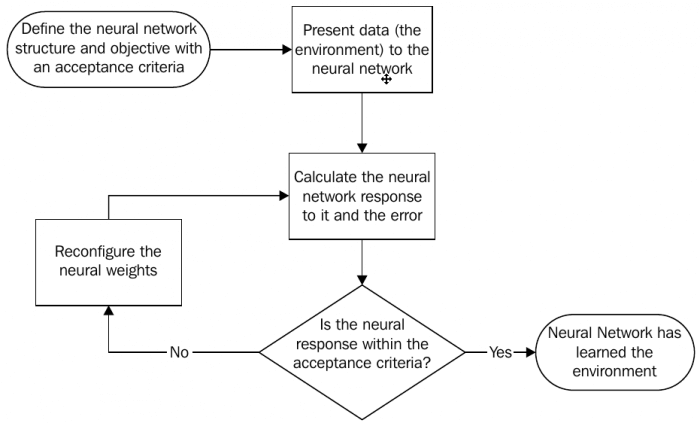
Как и другие программы, которые мы хотим написать, нам следует определить нашу цель, таким образом здесь, мы говорим о нейронной сети для обучения некоторым знаниям. Нам следует предоставить эти знания(или среду) к искусственной нейронной сети и проверить его ответ, что естественно не имеет смысла. Ответ сети после сравнения с ожидаемым результатом и это скармливается функции стоимости(cost function) C. Эта функция стоимости определит, как весы W будут обновлены. Алгоритм обучения затем вычисляет ΔW, которая означает изменение значений добавленных весов. Весы будут обновлены по этой формуле:
W(k + 1) = W(k) + ΔW
Где k ссылается на k-ую итерацию и W(k) означает нейронные весы на k-ой итерации, и впоследствии k + 1 означает следующую итерацию.
Когда начнется процесс обучения нейронная сеть должна возвращает результат все ближе и ближе к ожидаемому, пока не достигнет удовлетворительной оценки. Обучающий алгоритм затем считается завершенным.
Два этапа обучения(learning) — тренировка(training) и тестирование(testing)
Хорошо, мы можем спросить сейчас, нейронная сеть заранее обучилась из данных, но как мы подтвердим, как она эффективно обучилась? Ответ такой же, как на экзаменах, которые сдают студенты; мы нуждаемся в проверке ответа после тренировки. Но постойте! Не считаете ли вы, что это похоже на то, как учитель кладет на экзамене такие же вопросы, показанные им в классе ученикам? Нет никакого смысла в оценке обучения кого-либо с примерами, которые он раньше знал или подозревающий учитель заключил, что ученик мог запомнить весь материал вместо того, чтобы его изучить.
Окей, позвольте сейчас объяснить этот момент. То, о чем мы сейчас говорим называется тестированием. Обучающий процесс, что мы покрыли называется тренировкой. После тренировки нейронной сети, нам следует протестировать ее обучена ли на самом деле. Для тестирования мы должны предоставить нейронной сети данные из другой части той же среды, из которой она обучалась. Это необходимо потому что, как и со студентами, нейронная сеть могла отвечать корректно только с теми точками данных, которые были предоставлены ей; это называется переобучение. Чтобы проверить если нейронная сеть не прошла на переобучение, мы должны проверить ее ответ на других точках данных.
Следующий рисунок иллюстрирует проблему переобучения. Представьте, что наша сеть спроектирована для аппроксимации некоторой функции f(x), точность которой неизвестна. Нейронная сеть скормлены некоторые данные из функции, что выдает следующий результат, показанный на рисунке слева. Тем не менее, расширяя область, мы замечаем, что нейронный ответ не соответствует данным.
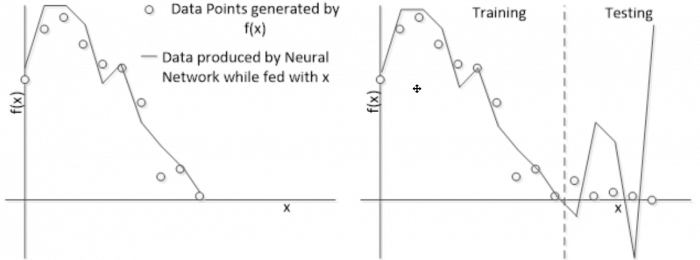
В этом случае мы видим, что нейронная сеть не обучилась всей среде(функция f(x)) Это случается по нескольким причинам:
- Нейронная сеть не получила достаточно информации с окружающей среды
- Данные из окружающей среды недетерминированы
- Тренировочные и тестовые датасеты плохо определены
- Нейронная сеть обучалась много на тренировочных данных, забыв о тестовых
В этой книге мы разберем этот процесс, предотвращая этот и другие вопросы, что могут возникнуть в течение тренировки.
Детали — параметры обучения
Процесс обучения может быть, и рекомадован, контролирован. Один важный параметр это скорость обучения, который часто представлен греческой буквой η. Этот параметр означает насколько сильно весы нейрона могут варьироваться в гиперпространстве весов. Давайте представим нейронную сеть с двумя входами и одним нейроном и следовательно одним выходом. Так мы получили два веса w1 и w2. Давайте теперь предположим, что мы хотим натренировать эту сеть и представим могли бы мы оценить ошибку между этой парой весов. Предположим что мы нашли поверхность похожий на следующий рисунок:
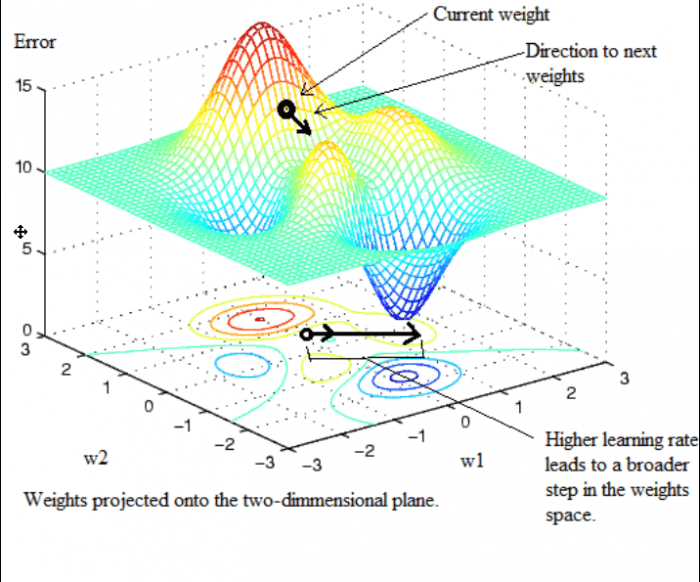
Скорость обучения отвечает за регуляцию наколько быстро будут двигаться на поверхности. Это может ускорить процесс обучения, но может вести к весам похуже, чем раньше.
Другой немаловажный параметр это условие для остановки. Обычно обучение заканчивается, когда общая средняя ошибка достигнута, но в некоторых случаях в сети не обучается и здесь малые или вообще нет изменений в весах. В последнем случае максимальное количество итераций или эпох это и есть условие остановки.
Измерение ошибки и функция стоимости
Это очень важно для успешного обучения в обучении с учителем. Давайте предположим, что представляем для сети множество N, состоящее из пар X и T, где X входо-независимые значения и T целевые значения зависимые от X. Давайте посчитаем, что нейронная сеть это математическая функция ANN(), выводящая Y на выходе, где скормлены значения X.
y = ANN(X)
На каждое X скормленное ANN оно выводит y, которое сравнивается с t и выводится ошибка e.
e = y — t
Тем не менее это индивидуальная ошибка для каждой точки данных. Нам следует в расчет взять основное измерение, включающая все пары N, потому что мы хотим обучить сеть всем данным и весы должны выводить данные, входящие в обучающую выборку. Эту роль берет функция стоимости:
C(X, T, W) = 1/N Σ[ANN(x[i] — t[i])]2
Где X — входные данные, T — желаемые выводы, W — веса, x[i] — вход на i-ый момент и t[i] — целевой выход для i-ого момента. Результат этой функции это в общем и целом ошибка между целевыми выходами и нейронными выходами, и ее следует минимизировать.
Примеры алгоритмов обучения
Давайте теперь соединим теоритический контент, представленный в легких примерах алгоритмов обучения. В этой главе мы собираемся изучить две архитектуры нейронных сетей перцептрон и adaline. Оба легкие, состоящие из одного слоя.
Перцептрон
Перцептроны обучаются беря в расчет только значение ошибки между целевым и выходом и скорость обучения. Правило обновления показан:
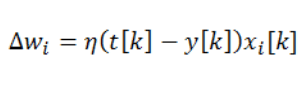
Где wi — это вес, соединенный с i-ым входом нейрона, t[k] — это целевой выход для k-ого примера, xi[k] — это i-ый вход для k-ого примера, и η — это скорость обучения. Это может быть показано очень легко и перцептрон не считается нелинейным в активационной функции. Он просто показывает направление ошибки в naive hope, что может закрыть задачу нейрона.
Правило дельта
Алгоритм получше основан на методе градиентного спуска, разработанный для нелинейности так же хорошо как и производная. Этот алгоритм дополняет перцептрон производной активационной функции g(h) c взвешенной суммой входов нейронов h перед тем как скормить их в активационной функции. Таким образом правило обновления выглядит так:
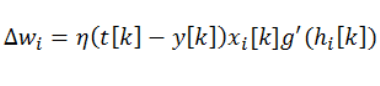
Программирование обучения нейросети
Теперь время разработать нейронную сеть используя концепты ООП и объяснить эту теорию. Проект показан в прошлой главе и адаптирована для перцептрона и adaline правила так же как и дельта правило.
Класс NeuralNet, представленный в прошлой главе был улучшен включив тренировочный датасет(вход и целевой выход), параметры обучения и активационную функцию. Функция InputLayer была улучшена и добавлен один метод. Мы добавили классы Adaline, Perceprtron, Training в проект. Детали реализации можете посмотреть в коде. Тем не менее давайте свяжем нейронное обучение и реализацию на Java класса Training.
Реализация параметра обучения
Класс Training сделан для тренировки нейронной сети. В этой главе мы собираемся использовать этот класс для тренировки классов Perceptron и Adaline. Также использованы активационные функции. Теперь давайте опрделим два перечисления для управления настройками:
public enum TrainingTypesENUM {
PERCEPTRON, ADALINE;
}
public enum ActivationFncENUM {
STEP, LINEAR, SIGLOG, HYPERTAN;
}
Добавляя эти параметры нам нужно определить условие окончания, ошибку, MSE ошибку и количество эпох:
private int epochs;
private double error;
private double mse;
Скорость обучения ранее добавлен в класс класс NeuralNet и будет использоваться здесь.
И наконец нам необходимо обновить веса в нейроне. Давайте посмотрим метод CalcNewWeight:
private double calcNewWeight(TrainingTypesENUM trainType,
double inputWeightOld, NeuralNet n, double error,
double trainSample, double netValue) {
switch (trainType) {
case PERCEPTRON:
return inputWeightOld + n.getLearningRate() * error * trainSample;
case ADALINE:
return inputWeightOld + n.getLearningRate() * error *
trainSample * derivativeActivationFnc(n.getActivationFnc(), netValue);
default:
throw new IllegalArgumentException(trainType
+ » does not exist in TrainingTypesENUM»);
}
}
Мы видим что выбирается процедура обновления для типа обучения(Adaline, Perceptron). Мы также видим параметры inputWeightOld(старые веса) n(нейросеть в процессе обучения), error(разница между целевым и выходом нейрона), trainSample(вход для веса), и netValue(взвешенная сумма перед обработкой активационной функцией). Скорость обучения можно получить методом getLearningRate() класса NeuralNet.
Еще одна интересная деталь это производная активационной функции, которая добавлена в типе Adaline, это и есть Delta rule. Все активационные функции реализованы в классе Training, и их производные. Метод derivativeActivationFnc помогает вызвать производные активационных функций.
Процедура обучения
Два специальных метода реализованы в классе Training: один для тренировки сети другой для тренировки нейронов в слое. Хотя это необязательно в этой главе, это всегда хорошо иметь код для будущих преобразований. Посмотрите бегло на реализвацию:
public NeuralNet train(NeuralNet n) {
ArrayList<Double> inputWeightIn = new ArrayList<Double>();
int rows = n.getTrainSet().length;
int cols = n.getTrainSet()[0].length;
while (this.getEpochs() < n.getMaxEpochs()) {
double estimatedOutput = 0.0;
double realOutput = 0.0;
for (int i = 0; i < rows; i++) {
double netValue = 0.0;
for (int j = 0; j < cols; j++) {
inputWeightIn = n.getInputLayer().getListOfNeurons().get(j).getListOfWeightIn();
double inputWeight = inputWeightIn.get(0);
netValue = netValue + inputWeight * n.getTrainSet()[i][j];
}
estimatedOutput = this.activationFnc(n.getActivationFnc(),
netValue);
realOutput = n.getRealOutputSet()[i];
this.setError(realOutput — estimatedOutput);
if (Math.abs(this.getError()) > n.getTargetError()) {
// fix weights
InputLayer inputLayer = new InputLayer();
inputLayer.setListOfNeurons(this.teachNeuronsOfLayer(cols,i, n, netValue));
n.setInputLayer(inputLayer);
}
this.setMse(Math.pow(realOutput — estimatedOutput, 2.0));
n.getListOfMSE().add(this.getMse());
this.setEpochs(this.getEpochs() + 1);
}
n.setTrainingError(this.getError());
return n;
}
Этот метод получает в параметре нейронную сеть и выводит другую сеть с обученными весами. Далее мы видим пока количество эпох не достигнет максимума в классе Training цикл while не завершится. Внутри цикла в цикле for высчитывается выход для входа в текущей итерации.
Когда получается конечный результат сравнивается с ожидаемым результатом и высчитывается ошибка. Если ошибка больше минимальной ошибки, то начинается обновление процедуры вызовом метода teachNeuronsInLayer.
inputLayer.setListOfNeurons(this.teachNeuronsOfLayer(cols, i, n, netValue));
Реализация этого метода прикреплен к этой главе.
Затем процесс заканчивается, когда эпохи закончились.
Определения классов
Следующие классы и методы покрытые в этой главе:
Имя класса: Adaline
| Название класса: Training | |
| Заметка: этот абстрактный и не может быть проинициализирован | |
| Атрибуты | |
| private int epochs | Целочисленное значение для хранения тренировочного цикла |
| private double error | Дробное значение для хранения разницы между ожидаемым результатом и выходом |
| private double mse | Дробное значение для среднеквадратичной ошибки |
| Перечисления | |
| Заметка: перечисления помогают контролировать разные типы | |
| public enum TrainingTypesENUM { PERCEPTRON, ADALINE; } |
Тренировочные типы |
| public enum ActivationFncENUM { STEP, LINEAR, SIGLOG, HYPERTAN; } |
Активационные функции |
| Методы | |
| public NeuralNet train(NeuralNet n) |
Тренирует сеть |
| Параметры: нетренированная нейросеть | |
| Возвращает: натренированная нейросеть | |
| public ArrayList teachNeuronsOfLayer(int numberOfInputNeurons, int line, NeuralNet n, double netValue) |
Обучает нейроны в слое вычисляя изменения в весах |
| Параметры: количество входных нейронов, примеры линий, нейросеть, выход нейросети | |
| Возвращает: ArrayList нейронов | |
| private double calcNewWeight(TrainingTypesENUM trainType, double inputWeightOld, NeuralNet n, double error, double trainSample, double netValue) |
Вычисляет новые веса |
| Параметры: тип обучения, старый входной вес, Нейросеть, ошибка, пример тренировки, выходное значение сети | |
| Возвращает: новый вес | |
| public double activationFnc ( ActivationFncENUM fnc, double value) |
Использует активационную функцию |
| Параметры:Тип активационной функции, дробное значение | |
| Возвращает: значение активационной функции | |
| public double derivativeActivationFnc ( ActivationFncENUM fnc, double value) |
Вычисляет производную активационной функции |
| Параметры: Тип активационной функции, дробное значение | |
| Возвращает: производную активационной функции | |
| private double fncStep (double v) |
Шаговая функция |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double fncLinear (double v) |
Линейная функция |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double fncSigLog (double v) |
Высчитывает сигмоидную функцию |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double fncHyperTan (double v) |
Вычисляет гиперболический тангенс |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double derivativeFncLinear (double v) |
Вычисляет производную линейной фукнции |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double derivativeFncSigLog (double v) |
Вычисляет производную сигмоидной функции |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| private double derivativeFncHyperTanv(double) | Вычисляет производную гиперболического тангенса |
| Параметры: дробное значение | |
| Возвращает: дробное значение | |
| public void printTrainedNetResult (NeuralNet trainedNet) |
Печатает результат тренированной сети |
| Параметры: нейросеть | |
| Возвращает: ничего | |
| Реализация класса Training.java | |
| Имя класса: Перцептрон | |
| Заметка: этот класс наследует атрибуты и методы класса Training | |
| Атрибуты | |
| Нет | |
| Методы | |
| public NeuralNet train(NeuralNet n) | Тренирует сеть |
| Параметры: нейросеть до тренировки | |
| Возвращает: нейросеть после тренировки | |
| Реализация класса Perceptron.java | |
| Заметка: этот класс наследует атрибуты и методы класса Training | |
| Атрибуты | |
| Нет | |
| Методы | |
| public NeuralNet train(NeuralNet n) | Тренирует сеть |
| Параметры: нейросеть до тренировки | |
| Возвращает: нейросеть после тренировки | |
| Реализация класса Adaline.java | |
| Имя класса: InputLayer | |
| Заметка: Этот класс обновлен | |
| Атрибуты | |
| Нет | |
| Методы | |
| public void setNumberOfNeuronsInLayer(int numberOfNeuronsInLayer) | Утсанавливает количество нейронов в слое |
| Реализация класса InputLayer.java | |
| Имя класса: NeuralNet | |
| Заметка: этот класс обновлен | |
| Атрибуты | |
| private double[][] trainSet | Матрица для хранения обучающего множества входных данных |
| private double[] realOutputSet | Вектор для хранения выходных данных |
| private int maxEpochs | Максимальное количество эпох |
| private double learningRate | Скорость обучения |
| private double targetError | целевая ошибка |
| private double trainingError | тренировочная ошибка |
| private TrainingTypesENUM trainType | тип тренировки |
| private ActivationFncENUM activationFnc | активационные функции |
| private ArrayList listOfMSE = new ArrayList() | список MSE ошибок |
| Методы | |
| public NeuralNet trainNet(NeuralNet n) | Тренирует нейросеть |
| Параметры: нейросеть | |
| Возвращает: обученную нейросеть | |
| public void printTrainedNetResult (NeuralNet n) | Печатает натренированную сеть |
| Параметры: обученная нейросеть | |
| Возвращает: ничего | |
| public double[][] getTrainSet() | Возвращает тренировочную выборку |
| public void setTrainSet(double[][] trainSet) | Геттер |
| public double[] getRealOutputSet() | Геттер |
| public void setRealOutputSet(double[] realOutputSet) | Сеттер |
| public void setRealOutputSet(double[] realOutputSet) | Сеттер |
| Реализация класса NeuralNet.java | |
Обновленная диаграмма классов показана в следующей схеме.
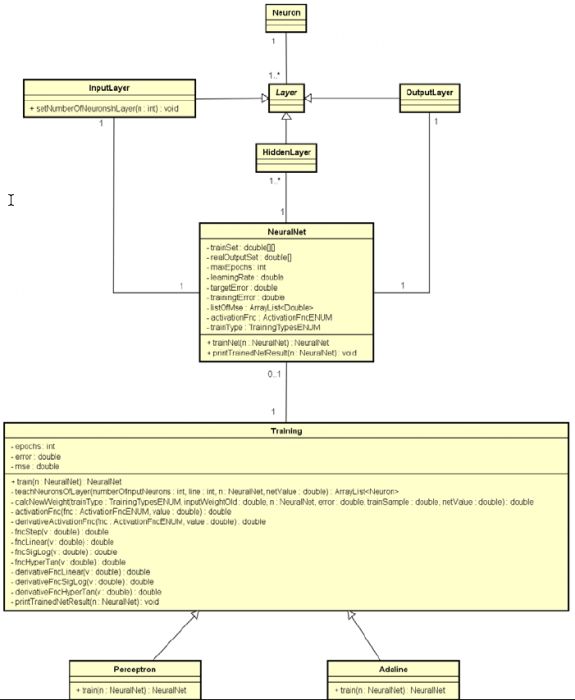
Два практических примера
Давайте посмотрим на два практическиз примера.
Перцептрон(предупреждающая система)
Чтобы облегчить понимание перцептрона давайте создадим предупреждающую систему. Она основана на логике AND. Здесь два сенсора следующих этим правилам:
- Если оба или один из них выключены, то сигнал запустится
- Если оба включены, то сигнал не запустится.
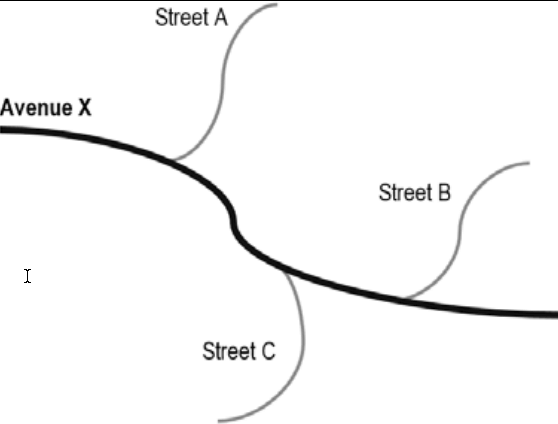
Эта логика показана в следующей картинке:
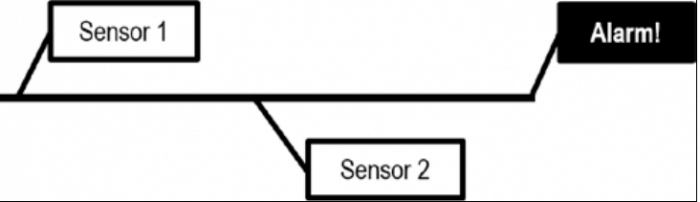
В схеме можно изобразить так:
| Пример | Сенсор 1 | Сенсор 2 | Результат |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 |
| 3 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 |
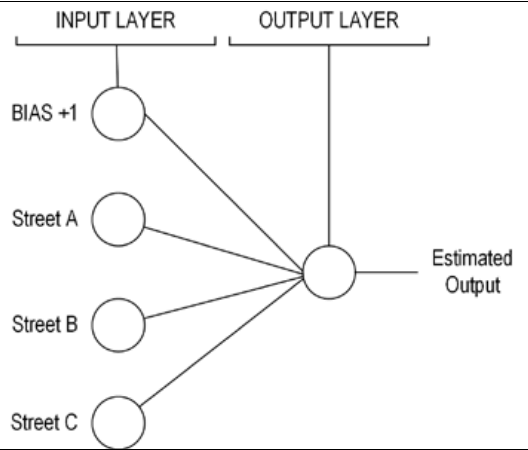
Рисунок Базовая система предупреждений показывает как организованы нейроны и слои для решения этой проблемы. Это архитектура нейросети:
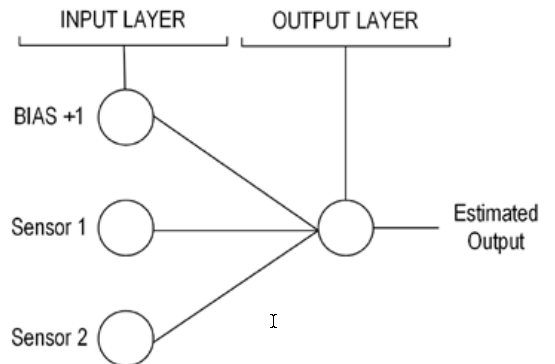
Давайте протестируем сеть:
private void testPerceptron() {
NeuralNet testNet = new NeuralNet();
testNet = testNet.initNet(2, 0, 0, 1);
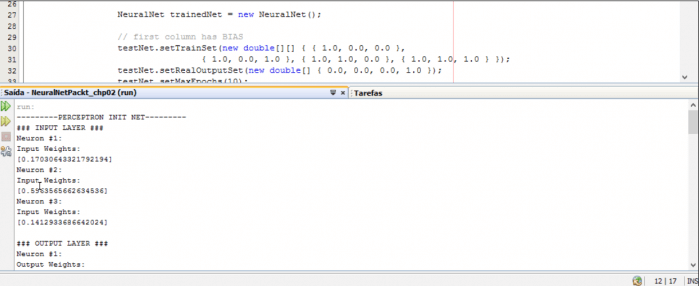
System.out.println(«———PERCEPTRON INIT NET———«);
testNet.printNet(testNet);
NeuralNet trainedNet = new NeuralNet();
// first column has BIAS
testNet.setTrainSet(new double[][] { { 1.0, 0.0, 0.0 },
{ 1.0, 0.0, 1.0 }, { 1.0, 1.0, 0.0 }, { 1.0, 1.0, 1.0 } });
testNet.setRealOutputSet(new double[] { 0.0, 0.0, 0.0, 1.0 });
testNet.setMaxEpochs(10);
testNet.setTargetError(0.002);
testNet.setLearningRate(1.0);
testNet.setTrainType(TrainingTypesENUM.PERCEPTRON);
testNet.setActivationFnc(ActivationFncENUM.STEP);
trainedNet = testNet.trainNet(testNet);
System.out.println();
System.out.println(«———PERCEPTRON TRAINED NET———«);
testNet.printNet(trainedNet);
System.out.println();
System.out.println(«———PERCEPTRON PRINT RESULT———«);
testNet.printTrainedNetResult(trainedNet);
}